Produsul încrucișat al vectorilor. Produs mixt al vectorilor
Definiție O colecție ordonată de (x 1 , x 2 , ... , x n) n numere reale se numește vector n-dimensional, și numerele x i (i = ) - componente, sau coordonate,
Exemplu. Dacă, de exemplu, o anumită fabrică de automobile trebuie să producă 50 de mașini, 100 de camioane, 10 autobuze, 50 de seturi de piese de schimb pentru mașini și 150 de seturi pentru camioane și autobuze pe schimb, atunci programul de producție al acestei fabrici poate fi scris ca vector (50, 100, 10, 50, 150), având cinci componente.
Notaţie. Vectorii sunt indicați cu litere mici aldine sau litere cu o bară sau săgeată în partea de sus, de ex. A sau. Cei doi vectori sunt numiți egal, dacă au același număr de componente și componentele lor corespunzătoare sunt egale.
Componentele vectoriale nu pot fi schimbate, de exemplu, (3, 2, 5, 0, 1)și (2, 3, 5, 0, 1) vectori diferiți.
Operații pe vectori. Munca
X= (x 1 , x 2 , ... ,x n) printr-un număr realλ numit vectorλ X= (λ x 1, λ x 2, ..., λ x n).
CantitateX= (x 1 , x 2 , ... ,x n) și y= (y 1 , y 2 , ... ,y n) se numește vector x+y= (x 1 + y 1 , x 2 + y 2 , ... , x n + + y n).
Spațiu vectorial. N -spațiu vectorial dimensional R n este definit ca multimea tuturor vectorilor n-dimensionali pentru care sunt definite operatiile de inmultire cu numere reale si de adunare.
Ilustrație economică. Ilustrarea economică a spațiului vectorial n-dimensional: spațiu al mărfurilor (bunuri). Sub bunuri vom înțelege un bun sau un serviciu care iese la vânzare la un anumit moment într-un anumit loc. Să presupunem că există un număr finit n de bunuri disponibile; cantităţile fiecăruia dintre ele achiziţionate de consumator se caracterizează printr-un set de bunuri
X= (x 1 , x 2 , ..., x n),
unde x i desemnează cantitatea celui de-al i-lea bun cumpărat de consumator. Vom presupune că toate bunurile au proprietatea divizibilității arbitrare, astfel încât orice cantitate nenegativă din fiecare dintre ele poate fi achiziționată. Atunci toate seturile posibile de bunuri sunt vectori ai spațiului bunurilor C = ( X= (x 1 , x 2 , ... , x n) x i ≥ 0, i = ).
Independență liniară.
Sistem e 1 , e 2 , ... , e se numesc m vectori n-dimensionali dependent liniar, dacă există astfel de numereλ 1 , λ 2 , ... , λ m , dintre care cel puțin unul este diferit de zero, astfel încât egalitateaλ 1 e 1 + λ 2 e 2 +... + λ m e m = 0; în caz contrar, acest sistem de vectori se numește liniar independent, adică egalitatea indicată este posibilă numai în cazul în care toate ![]() . Semnificația geometrică a dependenței liniare a vectorilor în R 3, interpretate ca segmente dirijate, explicați următoarele teoreme.
. Semnificația geometrică a dependenței liniare a vectorilor în R 3, interpretate ca segmente dirijate, explicați următoarele teoreme.
Teorema 1. Un sistem format dintr-un vector este dependent liniar dacă și numai dacă acest vector este zero.
Teorema 2. Pentru ca doi vectori să fie dependenți liniar, este necesar și suficient ca ei să fie coliniari (paraleli).
Teorema 3 . Pentru ca trei vectori să fie liniar dependenți, este necesar și suficient ca aceștia să fie coplanari (se află în același plan).
Triple stânga și dreapta ale vectorilor. Triplul vectorilor necoplanari a, b, c numit dreapta, dacă observatorul de la originea lor comună ocolește capetele vectorilor a, b, cîn ordinea dată pare să apară în sensul acelor de ceasornic. In caz contrar a, b, c -lăsat trei. Se numesc toate triplele din dreapta (sau stânga) ale vectorilor aceeași orientat.
Baza și coordonatele. Troica e 1, e 2 , e 3 vectori necoplanari în R 3 se numește bază, și vectorii înșiși e 1, e 2 , e 3 - de bază. Orice vector A poate fi extins în mod unic în vectori de bază, adică reprezentați sub formă
A= x 1 e 1+x2 e 2 + x 3 e 3, (1.1)
numerele x 1 , x 2 , x 3 din expansiune (1.1) se numesc coordonateAîn bază e 1, e 2 , e 3 și sunt desemnate A(x 1, x 2, x 3).
Baza ortonormala. Dacă vectorii e 1, e 2 , e 3 sunt perpendiculare pe perechi și lungimea fiecăruia dintre ele este egală cu unu, atunci baza se numește ortonormal, iar coordonatele x 1 , x 2 , x 3 - dreptunghiular. Vectorii de bază ai unei baze ortonormale vor fi notați cu i, j, k.
Vom presupune că în spațiu R 3 este selectat sistemul drept de coordonate carteziene dreptunghiulare (0, i, j, k}.
Opera de artă vectorială. Opera de artă vectorială A a vector b numit vector c, care este determinată de următoarele trei condiții:
1. Lungimea vectorului c egal numeric cu aria unui paralelogram construit pe vectori AȘi b, adică
c=
|a||b| păcat( A^b).
2. Vector c perpendicular pe fiecare dintre vectori AȘi b.
3. Vectori A, bȘi c, luate în ordinea indicată, formează un triplu drept.
Pentru un produs încrucișat c se introduce denumirea c =[ab] sau
c = a
× b.
Dacă vectorii AȘi b sunt coliniare, apoi păcat( a^b) = 0 și [ ab] = 0, în special, [ aa] = 0. Produse vectoriale ale vectorilor unitari: [ ij]=k, [jk] = i, [ki]=j.
Dacă vectorii AȘi b specificate în bază i, j, k coordonate A(a 1, a 2, a 3), b(b 1, b 2, b 3), atunci

Munca mixta. Dacă produsul vectorial al doi vectori AȘi bînmulțit scalar cu al treilea vector c, atunci se numește un astfel de produs de trei vectori munca mixtași este indicată prin simbol A b c.
Dacă vectorii a, bȘi cîn bază i, j, k date de coordonatele lor
A(a 1, a 2, a 3), b(b 1, b 2, b 3), c(c 1, c 2, c 3), atunci
 .
.
Produsul mixt are o interpretare geometrică simplă - este un scalar, egal în valoare absolută cu volumul unui paralelipiped construit pe trei vectori dați.
Dacă vectorii formează un triplu drept, atunci produsul lor mixt este un număr pozitiv egal cu volumul indicat; dacă este un trei a, b, c - stânga, atunci a b c<0 и V = - a b c, prin urmare V =|a b c|.
Coordonatele vectorilor întâlniți în problemele din primul capitol se presupune că sunt date relativ la o bază ortonormală dreaptă. Vector unitar codirecțional cu vector A, indicat prin simbol A O. Simbol r=OM notat cu vectorul rază al punctului M, simbolurile a, AB sau|a|, | AB|se notează module de vectori AȘi AB.
Exemplu 1.2. Aflați unghiul dintre vectori A= 2m+4nȘi b= m-n, Unde mȘi n- vectorii unitari si unghiul dintre mȘi n egal cu 120 o.
Soluţie. Avem: cos φ = ab/ab ab =(2m+4n) (m-n) = 2m 2 - 4n 2 +2mn=
= 2 - 4+2cos120 o = - 2 + 2(-0,5) = -3; a = ; A 2 = (2m+4n) (2m+4n) =
= 4m 2 +16mn+16n 2 = 4+16(-0,5)+16=12, ceea ce înseamnă a = . b = ; b 2 =
= (m-n)(m-n) = m 2 -2mn+n 2 =
1-2(-0,5)+1 = 3, ceea ce înseamnă b = . În sfârșit avem: cosφ = = -1/2, φ = 120 o.
Exemplul 1.3.Cunoașterea vectorilor AB(-3,-2,6) și B.C.(-2,4,4),calculați lungimea altitudinii AD a triunghiului ABC.
Soluţie. Notând aria triunghiului ABC cu S, obținem:
S = 1/2 î.Hr. Apoi AD=2S/BC, BC= = ![]() = 6,
= 6,
S = 1/2| AB ×AC|.
AC=AB+BC, ceea ce înseamnă vector A.C. are coordonate
.
.
Exemplu 1.4 . Sunt dați doi vectori A(11,10,2) și b(4,0,3). Găsi vector unitar c, ortogonală la vectori AȘi bşi direcţionată astfel încât triplul ordonat al vectorilor a, b, c avea dreptate.
Soluţie.Să notăm coordonatele vectorului cîn raport cu o bază ortonormală dreaptă dată în termeni de x, y, z.
Deoarece c ⊥ a, c ⊥b, Acea ca= 0,cb= 0. După condiţiile problemei se cere ca c = 1 şi a b c >0.
Avem un sistem de ecuații pentru a afla x,y,z: 11x +10y + 2z = 0, 4x+3z=0, x 2 + y 2 + z 2 = 0.
Din prima și a doua ecuație ale sistemului obținem z = -4/3 x, y = -5/6 x. Înlocuind y și z în a treia ecuație, avem: x 2 = 36/125, de unde
x =±
. Folosind condiția a b c > 0, obținem inegalitatea

Ținând cont de expresiile pentru z și y, rescriem inegalitatea rezultată sub forma: 625/6 x > 0, ceea ce presupune că x>0. Deci, x = , y = - , z =- .
Vector unitar- Acest vector, a cărui valoare absolută (modul) este egală cu unitatea. Pentru a desemna un vector unitar, vom folosi indicele e. Deci, dacă este dat un vector A, atunci vectorul său unitar va fi vectorul A e. Acest vector unitar este îndreptat în aceeași direcție cu vectorul însuși A, iar modulul său este egal cu unu, adică a e = 1.
Evident, A= a A e (a - modul vectorial A). Aceasta rezultă din regula prin care se realizează operația de înmulțire a unui scalar cu un vector.
Vectori unitari adesea asociat cu axele de coordonate ale unui sistem de coordonate (în special, cu axele unui sistem de coordonate carteziene). Direcțiile acestora vectori coincid cu direcțiile axelor corespunzătoare, iar originile lor sunt adesea combinate cu originea sistemului de coordonate.
Lasă-mă să-ți amintesc asta Sistemul de coordonate cartezieneîn spațiu, se numește în mod tradițional un trio de axe reciproc perpendiculare care se intersectează într-un punct numit originea coordonatelor. Axele de coordonate sunt de obicei notate cu literele X, Y, Z și sunt numite axa absciselor, axa ordonatelor și, respectiv, axa aplicată. Descartes însuși a folosit o singură axă, pe care erau trasate abscisele. Meritul folosirii sisteme topoarele aparține elevilor săi. Prin urmare sintagma Sistemul de coordonate carteziene greșit din punct de vedere istoric. E mai bine să vorbim dreptunghiular sistem de coordonate sau sistem de coordonate ortogonal. Cu toate acestea, nu vom schimba tradițiile și în viitor vom presupune că sistemele de coordonate carteziene și dreptunghiulare (ortogonale) sunt unul și același.
Vector unitar, îndreptată de-a lungul axei X, se notează i, vector unitar, îndreptată de-a lungul axei Y, se notează j, A vector unitar, îndreptat de-a lungul axei Z, este notat k. Vectori i, j, k sunt numite orts(Fig. 12, stânga), au module unice, adică
i = 1, j = 1, k = 1.
Topoarele și vectori unitari sistem de coordonate dreptunghiularîn unele cazuri au denumiri și denumiri diferite. Astfel, axa de abscisă X poate fi numită axa tangentă, iar vectorul său unitar este notat τ (litera greacă mică tau), axa ordonatelor este axa normală, orth este notat n, axa aplicată este axa binormală, vectorul său unitar este notat b. De ce să schimbi numele dacă esența rămâne aceeași?
Faptul este că, de exemplu, în mecanică, atunci când se studiază mișcarea corpurilor, sistemul de coordonate dreptunghiular este folosit foarte des. Deci, dacă sistemul de coordonate însuși este staționar și modificarea coordonatelor unui obiect în mișcare este urmărită în acest sistem staționar, atunci de obicei axele sunt desemnate X, Y, Z și lor. vectori unitari respectiv i, j, k.
Dar adesea, atunci când un obiect se mișcă de-a lungul unei căi curbe (de exemplu, într-un cerc), este mai convenabil de luat în considerare procese mecaniceîntr-un sistem de coordonate care se deplasează cu acest obiect. Pentru un astfel de sistem de coordonate în mișcare sunt folosite alte nume de axe și vectorii lor unitari. Doar așa este. În acest caz, axa X este direcționată tangențial la traiectoria în punctul în care se află în prezent acest obiect. Și atunci această axă nu se mai numește axa X, ci axa tangentă, iar vectorul ei unitar nu mai este desemnat i, A τ . Axa Y este îndreptată de-a lungul razei de curbură a traiectoriei (în cazul mișcării într-un cerc - spre centrul cercului). Și deoarece raza este perpendiculară pe tangente, axa se numește axă normală (perpendiculară și normală sunt același lucru). Vectorul unitar al acestei axe nu mai este notat j, A n. A treia axă (fostă Z) este perpendiculară pe cele două anterioare. Acesta este un binormal cu orth b(Fig. 12, dreapta). Apropo, în acest caz așa sistem de coordonate dreptunghiular adesea denumite „naturale” sau naturale.
Definiție. Produsul vectorial al vectorului a (multiplicand) și al unui vector necoliniar (multiplicand) este al treilea vector c (produs), care este construit după cum urmează:
1) modulul său este numeric egal cu aria paralelogramului din fig. 155), construit pe vectori, adică este egal cu direcția perpendiculară pe planul paralelogramului menționat;
3) în acest caz, se alege direcția vectorului c (dintre două posibile) astfel încât vectorii c să formeze un sistem de dreapta (§ 110).
Denumire: sau
Adăugarea la definiție. Dacă vectorii sunt coliniari, atunci considerând că figura este (condițional) un paralelogram, este firesc să se atribuie o zonă zero. Prin urmare, produsul vectorial al vectorilor coliniari este considerat egal cu vectorul nul.

Deoarece vectorului nul i se poate atribui orice direcție, acest acord nu contrazice paragrafele 2 și 3 din definiție.
Observație 1. În termenul „produs vectorial” primul cuvânt indică faptul că rezultatul acțiunii este un vector (spre deosebire de un produs scalar; cf. § 104, observația 1).
Exemplul 1. Găsiți produsul vectorial în care sunt vectorii principali ai sistemului de coordonate drept (Fig. 156).
1. Deoarece lungimile vectorilor principali sunt egale cu o unitate de scară, aria paralelogramului (pătratului) este numeric egală cu unu. Aceasta înseamnă că modulul produsului vectorial este egal cu unu.
2. Deoarece perpendiculara pe plan este o axă, produsul vectorial dorit este un vector coliniar cu vectorul k; și deoarece ambele au modulul 1, produsul vectorial dorit este egal fie cu k, fie cu -k.
3. Dintre acești doi vectori posibili trebuie ales primul, întrucât vectorii k formează un sistem dreptaci (iar vectorii unul stânga).
Exemplul 2. Găsiți produsul încrucișat
Soluţie. Ca și în exemplul 1, concluzionăm că vectorul este egal fie cu k, fie cu -k. Dar acum trebuie să alegem -k, deoarece vectorii formează un sistem dreptaci (iar vectorii formează unul stânga). Asa de,
Exemplul 3. Vectorii au lungimi egale cu 80, respectiv 50 cm și formează un unghi de 30°. Luând metrul ca unitate de lungime, găsiți lungimea produsului vectorial a

Soluţie. Aria unui paralelogram construit pe vectori este egală cu Lungimea produsului vectorial dorit este egală cu
Exemplul 4. Aflați lungimea produsului vectorial al acelorași vectori, luând centimetri ca unitate de lungime.
Soluţie. Deoarece aria unui paralelogram construit pe vectori este egală, lungimea produsului vectorial este egală cu 2000 cm, adică.
Dintr-o comparație a exemplelor 3 și 4 este clar că lungimea vectorului depinde nu numai de lungimile factorilor, ci și de alegerea unității de lungime.
Semnificația fizică a unui produs vectorial. Dintre numeroasele mărimi fizice reprezentate de produsul vectorial, vom lua în considerare doar momentul forței.
Fie A punctul de aplicare al forței. Momentul forței relativ la punctul O se numește produs vectorial. Deoarece modulul acestui produs vectorial este numeric egal cu aria paralelogramului (Fig. 157), atunci modulul momentului este egal cu produsul dintre bază și înălțime, adică forța înmulțită cu distanța de la punctul O la dreapta de-a lungul căreia acționează forța.
În mecanică, este dovedit că pentru ca un corp rigid să fie în echilibru, este necesar ca nu numai suma vectorilor reprezentând forțele aplicate corpului să fie egală cu zero, ci și suma momentelor de forță. În cazul în care toate forțele sunt paralele cu un plan, adunarea vectorilor reprezentând momente poate fi înlocuită prin adăugarea și scăderea mărimilor acestora. Dar cu direcții arbitrare ale forțelor, o astfel de înlocuire este imposibilă. În conformitate cu aceasta, produsul vectorial este definit exact ca un vector, și nu ca un număr.

Înainte de a da conceptul de produs vectorial, să ne întoarcem la întrebarea orientării unui triplu ordonat al vectorilor a →, b →, c → în spațiul tridimensional.
Pentru început, să lăsăm deoparte vectorii a → , b → , c → dintr-un punct. Orientarea triplei a → , b → , c → poate fi dreapta sau stânga, în funcție de direcția vectorului c → însuși. Tipul de triplă a → , b → , c → va fi determinat din direcția în care se face cea mai scurtă tură de la vectorul a → la b → de la capătul vectorului c → .
Dacă virajul cel mai scurt este efectuat în sens invers acelor de ceasornic, atunci triplul vectorilor a → , b → , c → se numește dreapta, dacă în sensul acelor de ceasornic - stânga.
În continuare, luăm doi vectori necoliniari a → și b →. Să reprezentăm apoi vectorii A B → = a → și A C → = b → din punctul A. Să construim un vector A D → = c →, care este simultan perpendicular atât pe A B → cât și pe A C →. Astfel, atunci când construim vectorul în sine A D → = c →, putem face două lucruri, dându-i fie o direcție, fie invers (vezi ilustrația).
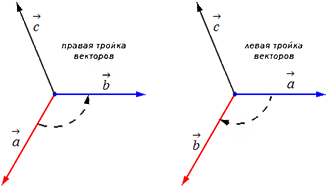
Un triplu ordonat al vectorilor a → , b → , c → poate fi, după cum am aflat, la dreapta sau la stânga în funcție de direcția vectorului.
Din cele de mai sus putem introduce definiția unui produs vectorial. Această definiție este dată pentru doi vectori definiți într-un sistem de coordonate dreptunghiular al spațiului tridimensional.
Definiția 1
Produsul vectorial al doi vectori a → și b → vom numi un astfel de vector definit într-un sistem de coordonate dreptunghiular al spațiului tridimensional astfel încât:
- dacă vectorii a → și b → sunt coliniari, va fi zero;
- va fi perpendicular atât pe vectorul a → cât și pe vectorul b → adică. ∠ a → c → = ∠ b → c → = π 2 ;
- lungimea sa este determinată de formula: c → = a → · b → · sin ∠ a → , b → ;
- triplul vectorilor a → , b → , c → are aceeași orientare ca și sistemul de coordonate dat.
Produsul vectorial al vectorilor a → și b → are următoarea notație: a → × b →.
Coordonatele produsului vectorial
Deoarece orice vector are anumite coordonate în sistemul de coordonate, putem introduce o a doua definiție a unui produs vectorial, care ne va permite să găsim coordonatele acestuia folosind coordonatele date ale vectorilor.
Definiția 2
Într-un sistem de coordonate dreptunghiular al spațiului tridimensional produs vectorial al doi vectori a → = (a x ; a y ; a z) și b → = (b x ; b y ; b z) se numește vector c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , unde i → , j → , k → sunt vectori de coordonate.
Produsul vectorial poate fi reprezentat ca determinant al unei matrice pătrate de ordinul trei, unde primul rând conține vectorii vectori i → , j → , k → , al doilea rând conține coordonatele vectorului a → , iar al treilea rând conține coordonatele vectorului b → într-un sistem de coordonate dreptunghiular dat, acesta este determinantul matricei arată astfel: c → = a → × b → = i → j → k → a x a y a z b x b y b z
Expandând acest determinant în elementele primului rând, obținem egalitatea: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z · i → - a x a z b x b z · j → + a x a y b x b y · k → = = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →
Proprietățile unui produs încrucișat
Se știe că produsul vectorial în coordonate este reprezentat ca determinant al matricei c → = a → × b → = i → j → k → a x a y a z b x b y b z , apoi pe baza proprietățile determinantului matricei sunt afișate următoarele proprietățile unui produs vectorial:
- anticomutatie a → × b → = - b → × a → ;
- distributivitatea a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → sau a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
- asociativitatea λ a → × b → = λ a → × b → sau a → × (λ b →) = λ a → × b →, unde λ este un număr real arbitrar.
Aceste proprietăți au dovezi simple.
Ca exemplu, putem demonstra proprietatea anticomutativă a unui produs vectorial.
Dovada anticomutativității
Prin definiție, a → × b → = i → j → k → a x a y a z b x b y b z și b → × a → = i → j → k → b x b y b z a x a y a z . Și dacă două rânduri ale matricei sunt schimbate, atunci valoarea determinantului matricei ar trebui să se schimbe la opus, prin urmare, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , care și demonstrează că produsul vectorial este anticomutativ.
Produs vectorial - exemple și soluții
În cele mai multe cazuri, există trei tipuri de probleme.
În problemele de primul tip, lungimile a doi vectori și unghiul dintre ei sunt de obicei date și trebuie să găsiți lungimea produsului vectorial. În acest caz, utilizați următoarea formulă c → = a → · b → · sin ∠ a → , b → .
Exemplul 1
Aflați lungimea produsului vectorial al vectorilor a → și b → dacă cunoașteți a → = 3, b → = 5, ∠ a →, b → = π 4.
Soluţie
Determinând lungimea produsului vectorial al vectorilor a → și b →, rezolvăm această problemă: a → × b → = a → · b → · sin ∠ a → , b → = 3 · 5 · sin π 4 = 15 2 2 .
Răspuns: 15 2 2 .
Problemele de al doilea tip au o legătură cu coordonatele vectorilor, în ele produsul vectorial, lungimea acestuia etc. sunt căutate prin coordonatele cunoscute ale vectorilor dați a → = (a x; a y; a z) Și b → = (b x ; b y ; b z) .
Pentru acest tip de problemă, puteți rezolva o mulțime de opțiuni de activitate. De exemplu, nu pot fi specificate coordonatele vectorilor a → și b →, ci expansiunile lor în vectori de coordonate de forma b → = b x · i → + b y · j → + b z · k → și c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, sau vectorii a → și b → pot fi specificați prin coordonatele începutului lor și punctele finale.
Luați în considerare următoarele exemple.
Exemplul 2
Într-un sistem de coordonate dreptunghiular se dau doi vectori: a → = (2; 1; - 3), b → = (0; - 1; 1). Găsiți produsul lor încrucișat.
Soluţie
Prin a doua definiție, găsim produsul vectorial al doi vectori în coordonate date: a → × b → = (a y · b z - a z · b y) · i → + (a z · b x - a x · b z) · j → + ( a x · b y - a y · b x) · k → = = (1 · 1 - (- 3) · (- 1)) · i → + ((- 3) · 0 - 2 · 1) · j → + (2) · (- 1) - 1 · 0) · k → = = - 2 i → - 2 j → - 2 k → .
Dacă scriem produsul vectorial prin determinantul matricei, atunci soluția acestui exemplu arată astfel: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .
Răspuns: a → × b → = - 2 i → - 2 j → - 2 k → .
Exemplul 3
Aflați lungimea produsului vectorial al vectorilor i → - j → și i → + j → + k →, unde i →, j →, k → sunt vectorii unitari ai sistemului de coordonate carteziene dreptunghiulare.
Soluţie
Mai întâi, să găsim coordonatele unui produs vectorial dat i → - j → × i → + j → + k → într-un sistem de coordonate dreptunghiular dat.
Se știe că vectorii i → - j → și i → + j → + k → au coordonatele (1; - 1; 0) și respectiv (1; 1; 1). Să aflăm lungimea produsului vectorial folosind determinantul matricei, atunci avem i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .
Prin urmare, produsul vectorial i → - j → × i → + j → + k → are coordonate (- 1 ; - 1 ; 2) în sistemul de coordonate dat.
Găsim lungimea produsului vectorial folosind formula (vezi secțiunea despre găsirea lungimii unui vector): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6.
Răspuns: i → - j → × i → + j → + k → = 6 . .
Exemplul 4
Într-un sistem de coordonate carteziene dreptunghiulare, sunt date coordonatele a trei puncte A (1, 0, 1), B (0, 2, 3), C (1, 4, 2). Găsiți un vector perpendicular pe A B → și A C → în același timp.
Soluţie
Vectorii A B → și A C → au următoarele coordonate (- 1 ; 2 ; 2) și respectiv (0 ; 4 ; 1). După ce am găsit produsul vectorial al vectorilor A B → și A C →, este evident că este un vector perpendicular prin definiție atât pe A B → cât și pe A C →, adică este o soluție a problemei noastre. Să o găsim A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .
Răspuns: - 6 i → + j → - 4 k → . - unul dintre vectorii perpendiculari.
Problemele de al treilea tip sunt concentrate pe utilizarea proprietăților produsului vectorial al vectorilor. După aplicarea acesteia, vom obține o soluție la problema dată.
Exemplul 5
Vectorii a → și b → sunt perpendiculari și lungimile lor sunt 3 și, respectiv, 4. Aflați lungimea produsului vectorial 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → .
Soluţie
Prin proprietatea distributivă a unui produs vectorial, putem scrie 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →
Prin proprietatea asociativității, scoatem coeficienții numerici din semnul produselor vectoriale din ultima expresie: 3 · a → × a → + 3 · a → × - 2 · b → + - b → × a → + - b → × - 2 · b → = = 3 · a → × a → + 3 · (- 2) · a → × b → + (- 1) · b → × a → + (- 1) · (- 2) · b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →
Produsele vectoriale a → × a → și b → × b → sunt egale cu 0, deoarece a → × a → = a → · a → · sin 0 = 0 și b → × b → = b → · b → · sin 0 = 0, atunci 3 · a → × a → - 6 · a → × b → - b → × a → + 2 · b → × b → = - 6 · a → × b → - b → × a → . .
Din anticomutativitatea produsului vectorial rezultă - 6 · a → × b → - b → × a → = - 6 · a → × b → - (- 1) · a → × b → = - 5 · a → × b → . .
Folosind proprietățile produsului vectorial, obținem egalitatea 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .
Prin condiție, vectorii a → și b → sunt perpendiculari, adică unghiul dintre ei este egal cu π 2. Acum tot ce rămâne este să înlocuiți valorile găsite în formulele adecvate: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → · sin (a → , b →) = 5 · 3 · 4 · sin π 2 = 60 .
Răspuns: 3 a → - b → × a → - 2 b → = 60.
Lungimea produsului vectorial al vectorilor prin definiție este egală cu a → × b → = a → · b → · sin ∠ a → , b → . Deoarece se știe deja (din cursul școlii) că aria unui triunghi este egală cu jumătate din produsul lungimilor celor două laturi înmulțit cu sinusul unghiului dintre aceste laturi. În consecință, lungimea produsului vectorial este egală cu aria paralelogramului - un triunghi dublat, și anume produsul laturilor sub forma vectorilor a → și b →, așezați dintr-un punct, de sinusul lui unghiul dintre ele sin ∠ a →, b →.
Acesta este sensul geometric al unui produs vectorial.

Semnificația fizică a produsului vectorial
În mecanică, una dintre ramurile fizicii, datorită produsului vectorial, puteți determina momentul unei forțe față de un punct din spațiu.
Definiția 3
Prin momentul forței F → aplicat punctului B, relativ la punctul A, vom înțelege următorul produs vectorial A B → × F →.
Dacă observați o eroare în text, vă rugăm să o evidențiați și să apăsați Ctrl+Enter
7.1. Definiţia cross product
Trei vectori necoplanari a, b și c, luați în ordinea indicată, formează un triplet de dreapta dacă, de la sfârșitul celui de-al treilea vector c, se vede cea mai scurtă întoarcere de la primul vector a la al doilea vector b. fie în sens invers acelor de ceasornic, iar un triplet stângaci dacă este în sensul acelor de ceasornic (vezi Fig. 16).
Produsul vectorial al vectorului a și al vectorului b se numește vector c, care:
1. Perpendicular pe vectorii a și b, adică c ^ a și c ^ b;
2. Are o lungime egală numeric cu aria unui paralelogram construit pe vectorii a șib ca pe laterale (vezi Fig. 17), i.e.
3. Vectorii a, b și c formează un triplu dreptaci.


Produsul încrucișat este notat cu a x b sau [a,b]. Următoarele relații între vectorii unitari i rezultă direct din definiția produsului vectorial, jȘi k(vezi fig. 18):
i x j = k, j x k = i, k x i = j.
Să demonstrăm, de exemplu, că i xj =k.
1) k ^ i, k ^ j ;
2) |k |=1, dar | eu x j| = |i | |J | sin(90°)=1;
3) vectorii i, j și k formează un triplu drept (vezi Fig. 16).
7.2. Proprietățile unui produs încrucișat
1. La rearanjarea factorilor, produsul vectorial își schimbă semnul, adică. și xb =(b xa) (vezi Fig. 19).
Vectorii a xb și b xa sunt coliniari, au aceleași module (aria paralelogramului rămâne neschimbată), dar sunt direcționați opus (triplii a, b, a xb și a, b, b x a de orientare opusă). Acesta este axb = -(b xa).
2. Produsul vectorial are o proprietate de combinare în raport cu factorul scalar, adică l (a xb) = (l a) x b = a x (l b).

Fie l >0. Vectorul l (a xb) este perpendicular pe vectorii a și b. Vector ( l topor b este de asemenea perpendiculară pe vectorii a și b(vectorii a, l dar se află în același plan). Aceasta înseamnă că vectorii l(a xb) și ( l topor b coliniare. Este evident că direcțiile lor coincid. Au aceeasi lungime:
De aceea l(a xb)= l un xb. Se dovedește în mod similar pentru l<0.
3. Doi vectori nenuli a și b sunt coliniare dacă și numai dacă produsul lor vectorial este egal cu vectorul zero, adică a ||b<=>și xb =0.

În special, i *i =j *j =k *k =0 .
4. Produsul vectorial are proprietatea de distribuție:
(a+b) xc = a xc + b xs.
Vom accepta fără dovezi.
7.3. Exprimarea produsului încrucișat în termeni de coordonate
Vom folosi tabelul cu produse încrucișate a vectorilor i, jși k:

dacă direcția căii celei mai scurte de la primul vector la al doilea coincide cu direcția săgeții, atunci produsul este egal cu al treilea vector; dacă nu coincide, al treilea vector este luat cu semnul minus.
Fie dați doi vectori a =a x i +a y j+a z kși b =b x i+b y j+b z k. Să găsim produsul vectorial al acestor vectori înmulțindu-i ca polinoame (în funcție de proprietățile produsului vectorial):

![]()
Formula rezultată poate fi scrisă și mai pe scurt:

întrucât partea dreaptă a egalității (7.1) corespunde expansiunii determinantului de ordinul trei în ceea ce privește elementele primului rând.Egalitatea (7.2) este ușor de reținut.
7.4. Unele aplicații ale produsului încrucișat
Stabilirea coliniarității vectorilor

Aflarea ariei unui paralelogram și a unui triunghi
Conform definiţiei produsului vectorial al vectorilor Ași b |a xb | =|a | * |b |sin g, adică S perechi = |a x b |. Și, prin urmare, D S =1/2|a x b |.
Determinarea momentului de forță în jurul unui punct
Fie aplicată o forță în punctul A F =AB lăsați-l să plece DESPRE- un punct din spațiu (vezi Fig. 20).

Din fizică se știe că moment de forta F relativ la punct DESPRE numit vector M, care trece prin punct DESPREȘi:
1) perpendicular pe planul care trece prin puncte O, A, B;
2) egal numeric cu produsul forței pe braț
3) formează un triplu drept cu vectorii OA și A B.
Prin urmare, M = OA x F.
Găsirea vitezei de rotație liniară
Viteză v punctul M al unui corp rigid care se rotește cu viteza unghiulară wîn jurul unei axe fixe, este determinată de formula lui Euler v =w xr, unde r =OM, unde O este un punct fix al axei (vezi Fig. 21).

